Statistical tools help us to better understand the world around us. They help us understand relationships between variables and test the efficiency of some environmental changes. Most people’s first introduction to statistics begins by learning hypothesis testing which is a method to test the validity of a commonly accepted claim about a population. In other words, you are trying to determine if you believe a statement to be true or false. That statement is the null hypothesis and the opposing statement is called the alternative hypothesis . The null hypothesis assumes there is no significant difference between the current population and the new population after some sort of intervention.
“A good hypothesis must be based on a good research question. It should be simple, specific and stated in advance.” (Hulley et al., 2001).
For example, if you want to test a new drug intervention for an autoimmune disease. In this case:
The null hypothesis is that the new drug has no effect on the symptoms of the disease.
The alternative hypothesis is that the drug is effective in alleviating symptoms of the disease.
Or, there are 2 schools A and B with 40,000 students each. And we want to compare the mean weights of students for both schools. In order to design this experiment, we need to choose a sample from both schools that accurately represents the entire population and conduct statistical tests after defining the Null and Alternate hypotheses:
Null hypothesis : There exists no difference in the mean weights of 2 schools
Alternative hypothesis : There exists some difference in the mean weights
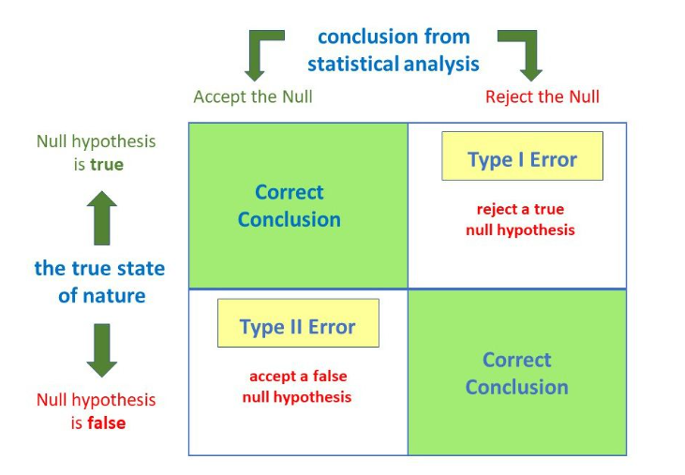
 The null hypothesis may or may not be rejected based on the data and the results of a statistical test. As these decisions are based on probabilities, there is always a risk of reaching the wrong conclusion. The error can be due to various reasons:
The null hypothesis may or may not be rejected based on the data and the results of a statistical test. As these decisions are based on probabilities, there is always a risk of reaching the wrong conclusion. The error can be due to various reasons:
- Small sample size
- Not chosen a well-representative sample
- Type I and Type II errors
A type I error is also known as a false positive and occurs when a researcher incorrectly rejects a true null hypothesis. A type II error is also known as a false negative and occurs when a researcher fails to reject a null hypothesis which is really false. Here a researcher concludes there is not a significant effect when actually there really is.
For example, if you decide to get tested for Covid-19 based on mild symptoms. There are two errors that could potentially occur:
Type I error (false positive): the test result says you have coronavirus, but you actually don’t.
Type II error (false negative): the test result says you don’t have coronavirus, but you actually do.
Let’s end this topic with a ridiculous but catchy example:

We hope this has cleared up the differences between a False Positive & False Negative.
At Caja, we have a wealth of experience and expertise with data-led organisational change. If you’d like to learn more about how we can support you, get in touch.
References:
- Browner, Warren S., et al. “Getting ready to estimate sample size: hypotheses and underlying principles.” Designing clinical research2 (1988): 51-63.
- Type I & Type II Errors | Differences, Examples, Visualizations (scribbr.com)